Decentralized Data Collection for Robotic Fleet Learning: A Game-Theoretic Approach
posted on February 26, 2024
By Oguzhan A.
Robotic Fleet Data Collection Through Game Theory
Motivation
In the rapidly evolving landscape of autonomous vehicles (AVs) and robotics, the efficient collection and utilization of data are crucial. Traditional data collection methods often lead to redundancy and inefficient use of bandwidth and storage. To deal with these challenges, we propose a strategic game between robots to sample data points to optimize data sampling, aiming to minimize the gap between current and target data distributions. This game-theoretic solution reaches a Nash equilibrium with only one message passing between AVs, offering an optimal strategy for data collection across robotic fleets.
The Challenge
AVs traditionally operate in isolation, prioritizing data collection based on individual, often greedy strategies. This isolation can lead to resource wastage and inefficiency. Coordination among AVs is essential to ensure the selection of the most valuable data points, avoiding redundancy and optimizing the collective data collection effort.
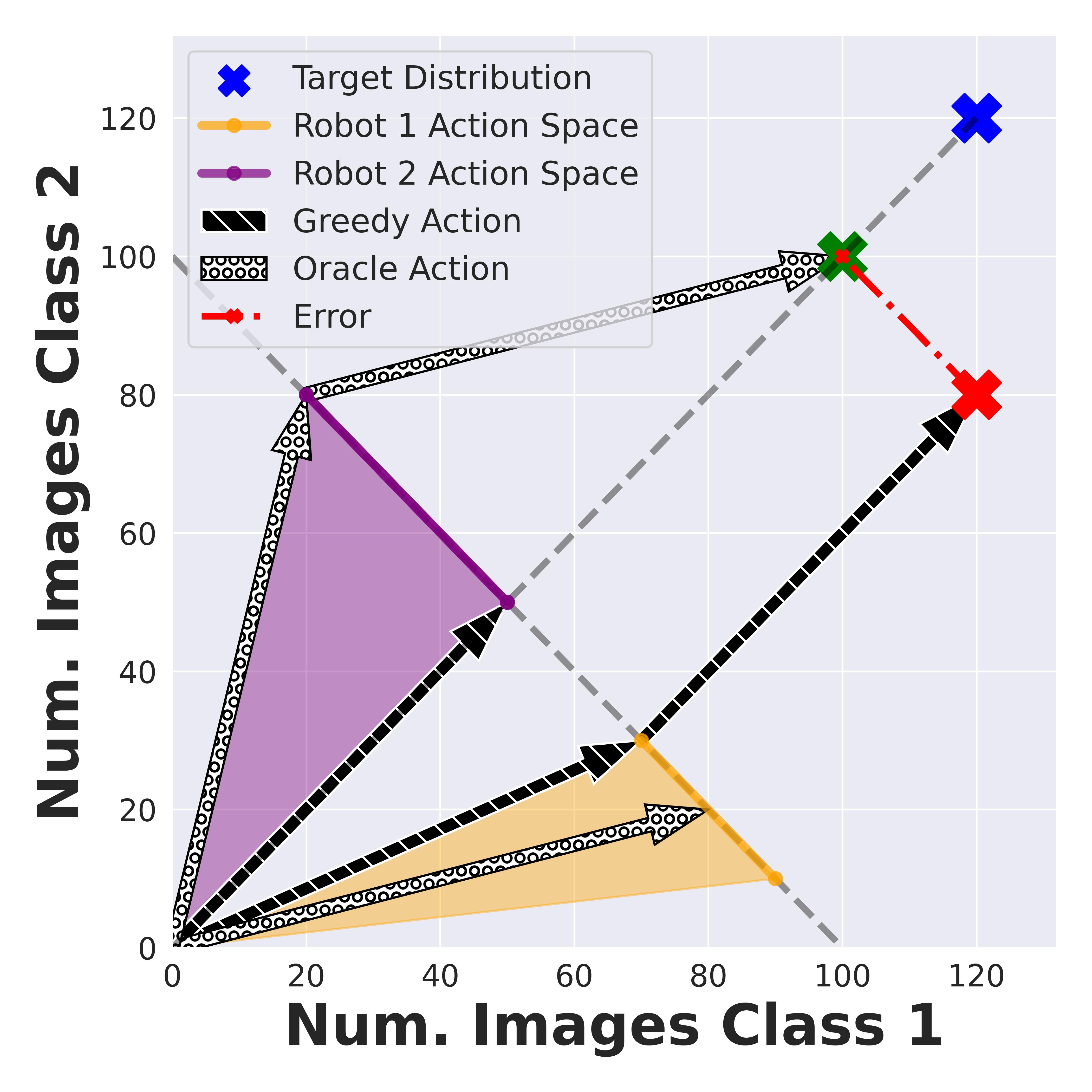
In the figure above, we show a toy example of why data collection needs to be coordinated. Here there are two robots observing data with only 2 classes. The axes represent the number of data points for each class. Our goal is to reach a target distribution (blue cross) where each class has 120 data points, represented by (120,120). The robots start at (0,0) with no data points in the cloud. The possible combinations that can be uploaded from robots 1 and 2 are shown as the shaded feasible action spaces (yellow and purple). This shaded region is determined by the robot’s local data distribution and vision model accuracy. Greedy (black) individually calculates the projection of the target distribution onto each robot’s feasible action space, but the sum of actions may not be optimal leading to a high error (red). However, Oracle accounts for the two robots’ action spaces and this minimizes the error between the target dataset and the sum of actions (grey).
A Game-Theoretic Solution
We frame the data collection problem as a potential game between networked AVs. Then, we show that this game reaches Nash equilibria based on the best-iterated response policy after only one message passings between the AVs. This equilibrium represents the collective optimization of data collection strategies, ensuring an optimal solution for the entire fleet.
How Interactive Policy Works
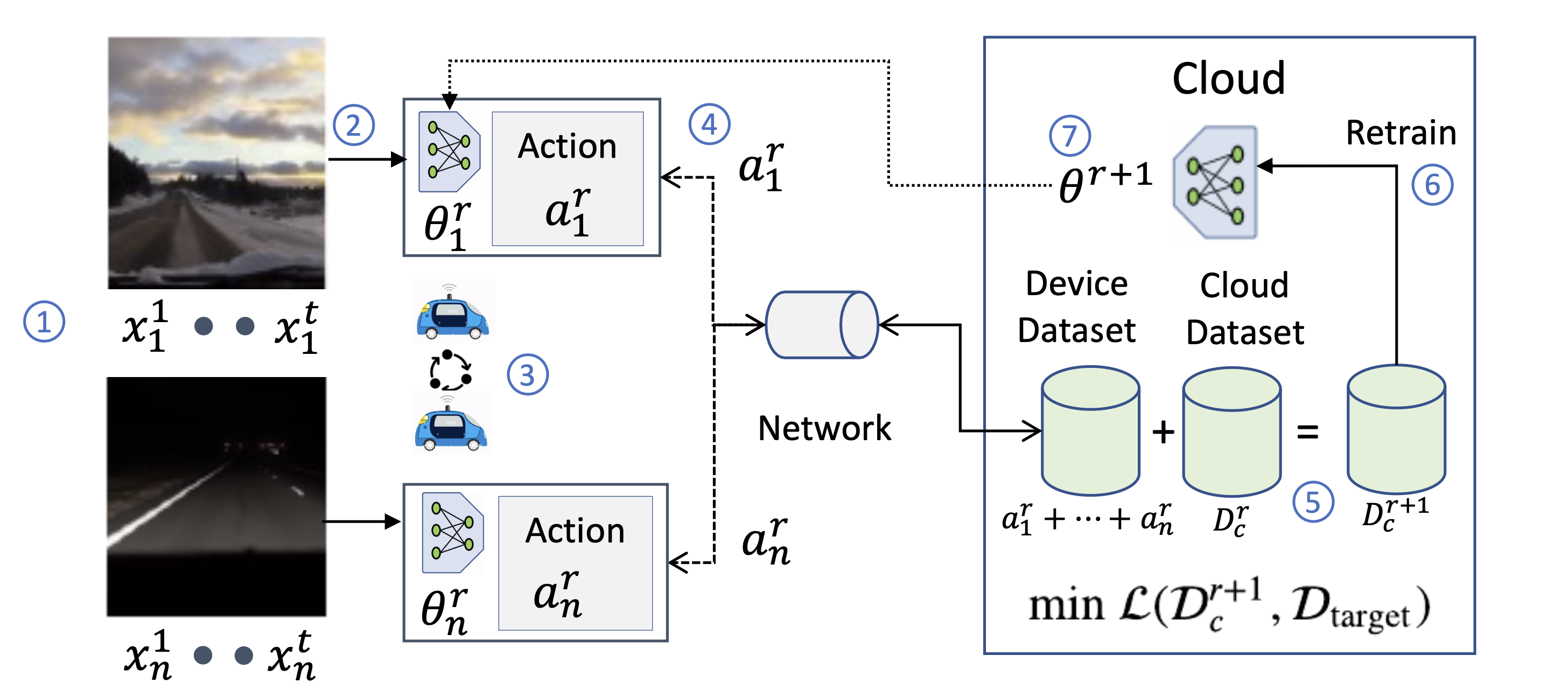
Each step in our cooperative algorithm is numbered in blue. First, each AV i observes a sequence of images in round r of data collection (step 1). Then, it classifies each image with a local vision model (step 2). Then it samples a limited set of images according to its action policy which governs what distribution of data points to upload. Crucially, the action to what data points to upload is chosen cooperatively with other AVs using a distributed optimization problem (step 3). Next, each AV transmits its local cache of data points to the cloud (step 4). The current cloud dataset is updated with the newly uploaded data points (step 5). The combined cloud dataset can be used to periodically retrain new model parameters (step 6), which are then downloaded by the AVs (step 7). All AVs share a goal of minimizing the distance between the collected cloud dataset and the target dataset.
Experimental Results
We show that our Interactive approach is able to achieve superior performance to the traditional distributed approach and achieves the same performance as an optimal Oracle policy. Our Interactive approach achieves performance improvements by up to 21% in classification accuracy compared to the standard benchmarks.
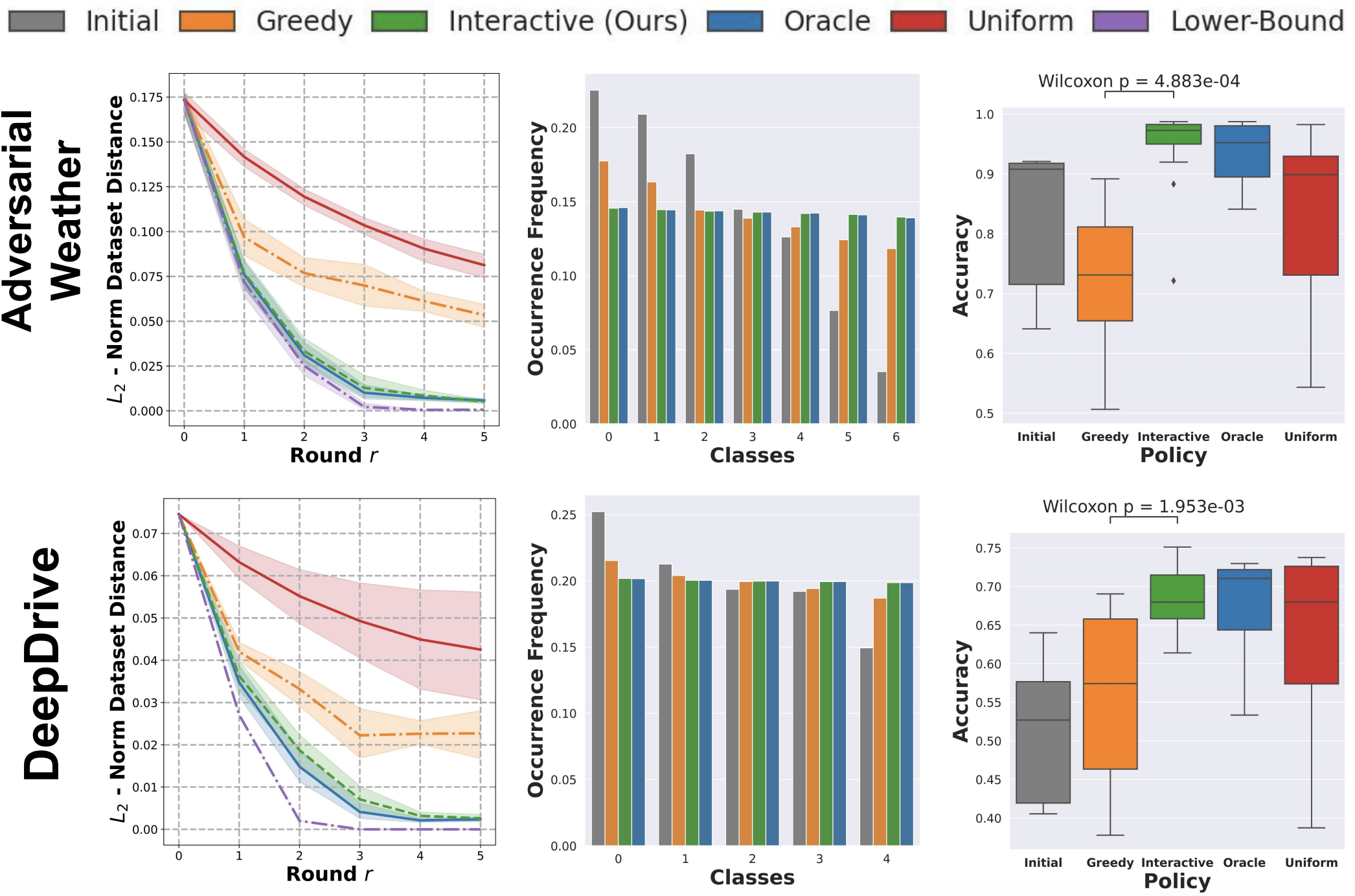
In the figure above, each row represents a different dataset. Column 1: As expected by our theory, Interactive minimizes the L2-norm distance (optimization objective, y-axis) better than Greedy and matches the omniscient Oracle. Column 2: Clearly, Interactive achieves a much more balanced distribution of classes (target distribution is uniform) than benchmarks. Column 3: Since Interactive achieves a more balanced dataset, this experimentally translates to a higher DNN accuracy (statistically significant) on a held-out test dataset.
Conclusion
Our work “Decentralized Data Collection for Robotic Fleet Learning” introduces a novel, theoretically grounded, cooperative data sampling policy for networked robotic fleets, which converges to an Oracle policy upon termination. Additionally, it converges in a single iteration under mild practical assumption, which allows communication efficiency on real-world datasets. Our approach is a first step towards an increasingly timely problem as today’s AV fleets measure terabytes of heterogeneous data in diverse operating contexts.