Fleet Supervisor Allocation: A Submodular Maximization Approach

Introduction

Today, robotic fleets are deployed across diverse industries, performing tasks ranging from autonomous driving to healthcare and package delivery. These robots are often trained in simulated environments and often struggle to adapt to real-world scenarios, making continuous data collection crucial for high performance.

A common method for training robots is Imitation Learning (IL), where humans supervise robots to perform tasks. However, a significant challenge arises when the number of robots far exceeds the number of human supervisors, necessitating assigning limited humans to the most informative robots..

Additionally, human supervision is often provided through teleoperation over a network, especially when robots are geographically distributed. This introduces challenges related to network reliability which can cause interruptions in data collection.

To address these challenges, we introduce Adaptive Submodular Allocation (ASA), a novel approach that optimizes human supervision in multi-robots systems by dynamically allocating supervisors based on informativeness and network reliability of each robot.

Problem: The Supervisor Allocation Problem

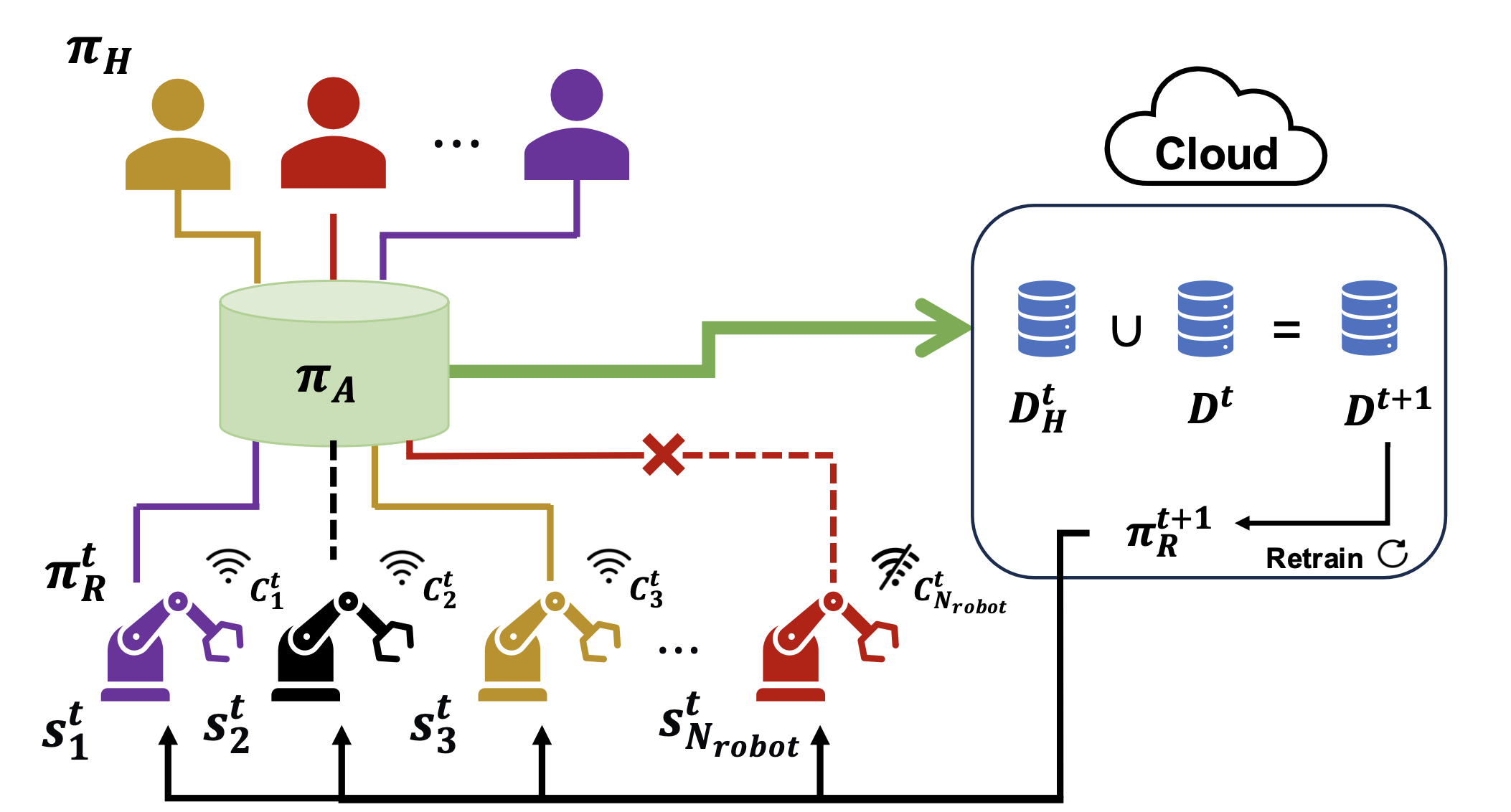
We consider a fleet of \(N_{robot}\) robots, operating with shared policy \(\pi_R^t\) at time \(t\), where each robot has its own state representation \(s_i^t \in S \). In each time step, human supervisors with policy \(\pi_H\) can be allocated to the robots based on the allocation policy \(\pi_A\). The allocation is subject to the network connectivity \(c_i^t\), which can be unreliable.

Here our objective is to find an allocation policy \(\pi_A\) that maximize the Return on Human Effort (RoHE) metric, which measures the performance of the robot fleet normalized by the human effort. This metric is proposed by Hoque et al. (2023) for Interactive Fleet Learning problem, and we extend it to account for uncertain network connectivity. Our objective can be formulated as:

\[\max_{\pi_A \in \Omega} \mathbb{E}_C \left[ \frac{N_{\text{human}}}{N_{\text{robot}}} \frac{\sum_{i \in I} \sum_{t=0}^T r(s_i^t, a^t_i)}{1 + \sum _{t=0}^T \| \pi_A(C^t, s^t, a^t, I) \|} \right]\]

Here \(T\) is the time horizon, \(r(s_i^t, a^t_i)\) is the reward function, and \(\Omega\) is the set of all allocation policies. The RoHE metric evaluates the efficiency of human supervision by considering both the rewards and human effort.

Our Approach: Adaptive Submodular Allocation (ASA)

Our approach, Adaptive Submodular Allocation (ASA), leverages submodular maximization to optimize the allocation of human supervisors to robots.

Why Submodular Maximization?

Submodular functions are well-suited for optimization problems where diminishing returns occur. In our context, the more similar the states of selected robots,the less new information we gain by selecting another robot from a similar state. Submodularity helps us formalize this diminishing returns principle.

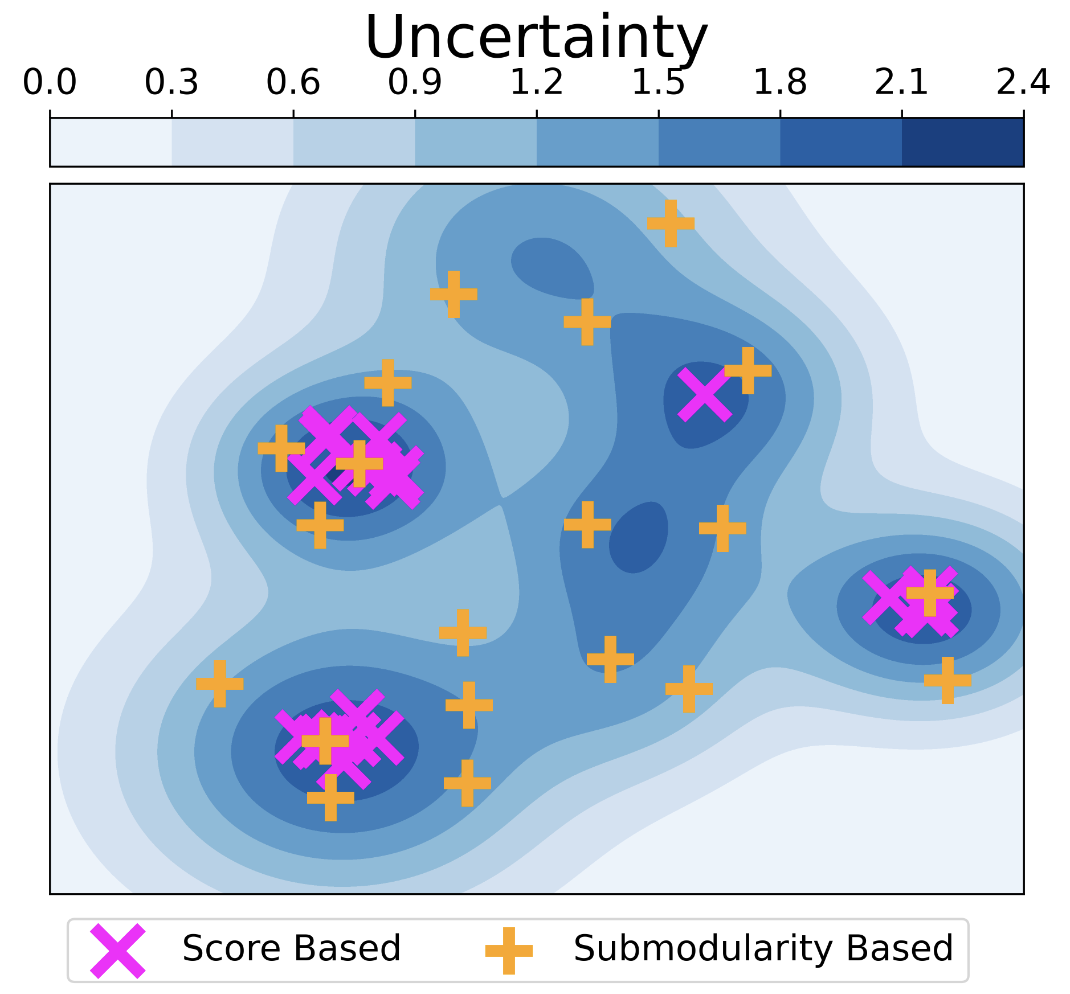
In the figure above, the blue contour represents uncertainty levels, with darker shades indicating higher uncertainty. Traditional score-based allocations (purple crosses) tend to select overlapping areas of high uncertainty resulting in redundant data collection. In constrast, submodular maximization (yellow plus signs) selects a more diverse set of robots, reducing redundancy while still capturing high uncertainty areas, leading to more informative data collection and better performance.

How ASA Works

We now explain how ASA works. We will first define the submodular objective function and then describe how ASA leverages this function to address the Fleet Supervisor Allocation problem.

Submodular Objective Function

Adaptive Submodular Allocation (ASA) leverages stochastic submodular maximization to address the Fleet Supervisor Allocation problem. The objective \(f_{C^t}(X)\) captures the value of supervising a set of robots \(X\) balancing diversity and informativeness:

\[f_{C^t}(X) = \sum_{i \in I} \max_{j \in X} c^t_j, M^t_{j,i}.\]

Here, \(c^t_j\) represents the connection reliability of robot \(j\) and \( M^t_{j,i} \) measures the value of supervision of robot \(j\) for robot \(i\). Here we define \( M_{j,i} \). However, the objective function \(f_{C^t}(X)\) is stochastic due to the uncertain network connectivity. Instead, we optimize the expected value of the objective function \(F(X) = \mathbb{E}_{C^t} [f_{C^t}(X)].\) Hence the problem becomes: \(\max_{X \subseteq I} F(X),\)

\[\text{subject to:} \; |X| \leq N_{\text{human}},\]

Adaptive Submodular Allocation (ASA) Policy

We now present our ASA policy which uses a greedy algorithm to iteratively select robots with the highest marginal gain based on the estimated expected value funtion, \(\widehat{F}\). The algorithm is as follows:

Starting with an empty set of selected robots, the algorithm iteratively selects the robot that provides the highest marginal gain in expected value function \(\widehat{F}\). If the marginal gain falls below a preset threshold or the number of selected robots reaches the number of human supervisors, the algorithm terminates.

Here the key component is the expected value function \(\widehat{F}\) which estimates the expected value of the submodular objective function \(F\). Initially, \(\widehat{F}\) is set to the connection probabilities and updated whenever a robot’s connection success is observed. This updating ensures ASA adapts to real-time network conditions.

The estimated value function \(\widehat{F}\) is defined as:

\[\widehat{F}(X) = \sum_c f_c(X) \widehat{p}_\xi,\]

where \(\widehat{p}_\xi\) represents the estimated connection probability of realization \( \xi \). The algorithm updates \(\widehat{p}_{\xi} \) after each allocation if observations on the allocations are available, dynamically improving allocation decisions.

This policy is shown to approximate the optimal solution with a factor of \(1 - 1/e\), providing robust and scalable performance across various network environments.

Experimental Results

We evaluated ASA in a simulated environment of 100 robots under various network conditions, including real-world 5G data. ASA outperformed benchmark methods, improving RoHE by up to 3.37× compared to traditional approaches, particularly in environments with unstable connectivity.

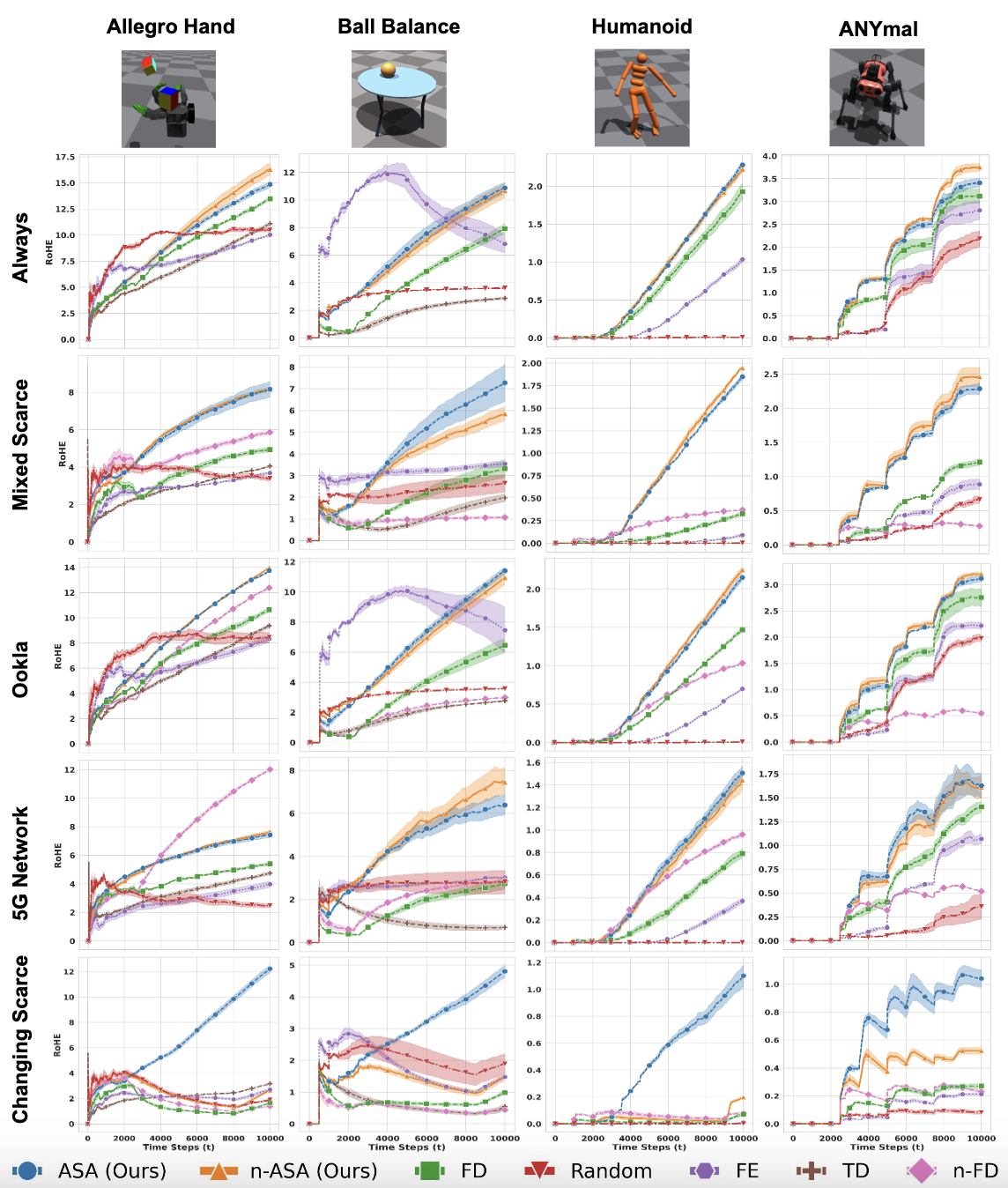
In the figure above, each column represents a different environment, while each row corresponds to a network configuration. We can see that ASA consistently outperforms other policies in terms of RoHE, demonstrating the effectiveness of our approach.

Conclusion

We introduce the ASA policy, offering a robust solution to the Fleet Supervisor Allocation problem. Our policy leverages stochastic submodular maximization to effectively balance human supervision and task performance across diverse environments. Through smarter allocation, ASA improves both fleet efficiency and data collection, laying the groundwork for more scalable autonomous fleets.