CSA: Bridging Modalities with Unimodal Power

Proceedings of the International Conference on Learning Representations (ICLR)

TLDR: This post introduces CSA, a novel method for bridging modalities with unimodal power. CSA leverages existing unimodal encoders to create a shared multimodal feature space, achieving competitive results with minimal training data and computational resources.

arXiv link

Code

Introduction

In the world of artificial intelligence, multimodal models like CLIP have shown impressive capabilities in tasks ranging from image classification to cross-modal retrieval. However, these models often demand enormous amounts of training data, which can be a significant challenge. What if we could achieve similar results with far less data and computation? That is the question that led us to develop Canonical Similarity Analysis (CSA).

The Challenge of Multimodal Learning

Multimodal models aim to create a shared feature space where data from different modalities (like images and text) can be compared. The traditional approach involves training models on massive datasets of paired multimodal data. For example, the original CLIP model was trained on 400 million image-text pairs, requiring significant computational resources. This approach also faces challenges with data quality, as internet-sourced data can be noisy or mislabeled.

Our Approach: Leveraging Unimodal Encoders

We hypothesized that we could build powerful multimodal encoders by leveraging existing, well-developed unimodal encoders. Unimodal encoders, like DINO for images and GTR for text, are trained on single modalities and require significantly less data than their multimodal counterparts. Our idea is to map the features from these unimodal encoders into a shared multimodal feature space using limited data.

System Plot:

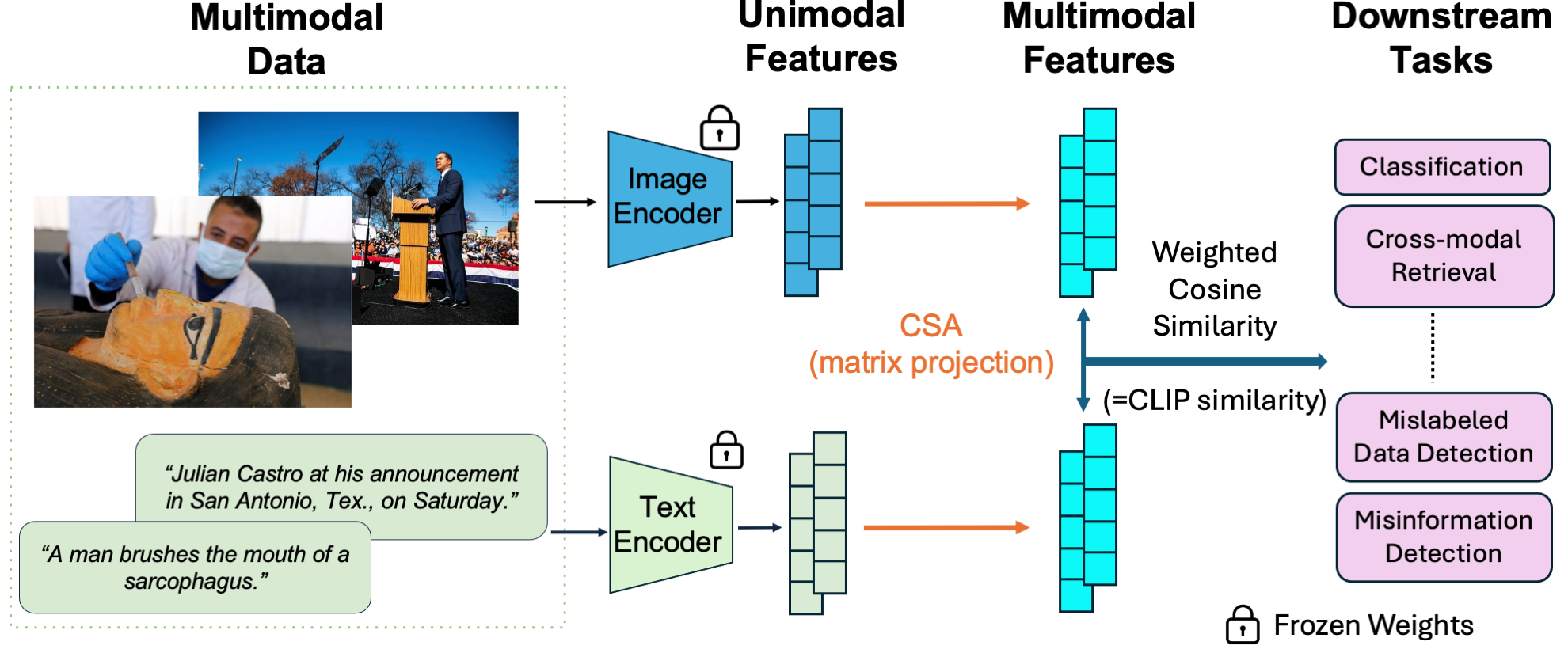
The CSA system works by first using pre-trained unimodal encoders to extract features from different modalities, such as images and text. These encoders, which have already been trained on large datasets of single-modality data, create a representation of the input in a feature space specific to their modality. Then, Canonical Correlation Analysis (CCA) is applied to these unimodal features. CCA identifies the dimensions of each unimodal feature space that are most correlated with each other. It finds linear transformations that project the unimodal features into a shared, lower-dimensional space. Finally, CSA calculates a weighted cosine similarity between the transformed features of different modalities, using the correlation coefficients derived from CCA as weights. This similarity score is used for various downstream tasks, such as classification and retrieval. The hyperparameter s controls how many dimensions are considered when calculating the weighted cosine similarity, allowing for a trade-off between noise reduction and retention of information. The entire process is achieved without any training of neural networks, making it highly efficient.

Introducing Canonical Similarity Analysis (CSA)

To achieve this, we developed Canonical Similarity Analysis (CSA). CSA uses two unimodal encoders to encode data into unimodal features, and then projects these features into a joint multimodal feature space. The core of CSA is its method for mapping unimodal features to a multimodal space and a novel similarity function for replicating CLIP’s similarity score. We use Canonical Correlation Analysis (CCA) to find the bases in each unimodal feature space that maximize correlation. This process involves a matrix decomposition without the need for training neural networks, making CSA computationally efficient. We then calculate a weighted cosine similarity in this space. By discarding information from less correlated bases, CSA focuses on the most relevant multimodal information. How CSA Works

Unimodal Encoding: First, we use pre-trained unimodal encoders to extract features from each modality.
CCA Mapping: Next, we use CCA to find the optimal linear transformations that map these features into a common space. CCA identifies the dimensions of the unimodal feature spaces that are most correlated and obtain the correlation coefficients.
Weighted Cosine Similarity: We then calculate a weighted cosine similarity score to measure the similarity of two multimodal data points, using the correlation coefficients as weights.

Data Efficiency and Performance

One of the most remarkable features of CSA is its data efficiency. In our experiments, CSA matched or exceeded the performance of CLIP in image classification, mislabeled data detection, and misinformation detection while requiring $50,000$ times less paired multimodal data for fine-tuning.

On ImageNet classification, CSA only needs $35,000$ training samples to match CLIP’s performance.
In Leafy Spurge classification, CSA outperformed CLIP with only $800$ training images.
CSA also showed superior performance in detecting mislabeled ImageNet images compared to CLIP, ASIF, and LLaVA.
We tested CSA on detecting misinformative news captions from the COSMOS dataset, and it outperformed both CLIP and ASIF.
We also showed that CSA is robust to noisy data. Even with $50\%$ of training labels randomly shuffled, CSA maintained a high level of accuracy.
We’ve demonstrated CSA’s versatility with modalities beyond image and text, including audio and text, paving the way for new modality pairs, such as lidar and text.

Limitations and Future Directions

While CSA is effective, it currently focuses on bimodal data, unlike models like ImageBind, which can handle six modalities. In addition, the performance of CSA relies on the quality of the unimodal encoders used. Our future work will explore:

Extending CSA to more than two modalities.
Understanding the relationship between the training set size and performance.
Fine-tuning the unimodal encoders for improved feature spaces.
Applying CSA to intramodal data, such as multi-view images.

Conclusion

CSA offers a compelling solution to the challenges of multimodal learning. By leveraging the power of unimodal encoders and using a novel similarity analysis method, CSA achieves competitive results with minimal training data and computational resources. We believe that CSA opens up new possibilities for efficient and robust multimodal machine learning towards binding emerging modalities.